Je poursuis la publication des chapitres de Principes des systèmes intelligents. J’en suis arrivé au type de modèle qui permettra de représenter une mémoire humaine parfaitement compatible avec la manière dont nous nous observons générant des phrases. Mais j’ai repeint le plancher de manière à ce point inepte que je vais me retrouver coincé dans un coin de la pièce : l’objet mathématique nécessaire n’existe pas ! Parviendrai-je à l’inventer ?
10. Le réseau mnésique
La démarche à entreprendre maintenant est tout à fait classique : après avoir constaté de quelle manière les signifiants s’enchaînent dans le discours, parole ou écriture – que les associations soient « induites » ou « libres » –, on va postuler que ces signifiants, ces mots, sont stockés en mémoire de la manière la plus économique possible qui permette à l’association de se produire de la façon qui a été observée. Ce que pourrait être ce mode de stockage, cette « représentation des connaissances », nous l’annoncions au quatrième chapitre :
« … sans avoir à définir des règles a priori qui déterminent les parcours légaux à l’intérieur du lexique, on peut imaginer que soient en place de manière constante des “chenaux”, des chréodes, des passages privilégiés pour se rendre d’un mot à l’autre. Par exemple qu’il existe un chenal qui conduise de “pharaon” à “pyramide” mais non de “pharaon” à “rhapsodie”, et que si l’on veut vraiment se rendre de “pharaon” à “rhapsodie” il faille faire un long détour à l’intérieur d’un lexique précontraint quant aux parcours possibles en son sein. Et il est plausible que l’apprentissage, c’est-à-dire la mise en mémoire des mots, s’opère de cette manière-là, par la création de chenaux. »
Autrement dit, dans le cas présent, la problématique dite de l’aviation doit être inversée. Rappelons qu’elle suppose que l’avion n’a pu être conçu que lorsqu’on a cessé de penser le vol d’une machine sur le modèle du vol des oiseaux : il faut au contraire penser que la machine ne pourra commencer à générer authentiquement des discours que lorsqu’elle le fera exactement de la même manière que nous.
Définir sur un lexique, un réseau dont les relations existant entre les objets représentent des passages obligés, constitue en soi une façon de réduire considérablement les manières possibles de parcourir cet espace, puisqu’il ne faut plus envisager désormais qu’un univers restreint d’« idées », d’enchaînements associatifs, au lieu d’une gigantesque combinatoire de mots. Bien sûr, des bifurcations existent au sein d’un réseau, qui obligent à opérer des choix si l’on veut définir sur lui le parcours unique correspondant à un discours particulier. De ce point de vue, la mise en place du réseau ne constitue qu’une première étape, une première simplification qui débouche sur une matrice réduite à partir de laquelle générer des discours singuliers – selon des principes qu’il faut alors définir.
Organiser une mémoire en réseau présente de nombreux avantages dont les principaux sont l’économie des moyens (maîtrise de la taille du système) et l’utilisation optimale des dispositions à l’auto-organisation de ce type de configuration. Par ailleurs, d’un point de vue purement informatique, l’utilisation de réseaux ne pose plus de problèmes particuliers : l’information peut être aisément stockée et actualisée sous la forme de « bases de données dynamiques » et d’excellents algorithmes de recherche applicables aux graphes sont connus.
Les réseaux sémantiques
L’idée d’utiliser le réseau pour représenter une information de type sémantique est déjà ancienne en IA. La notion de réseau sémantique est due à M. Ross Quillian. Il la présenta pour la première fois dans la thèse intitulée Semantic Memory qu’il défendit au Carnegie Institute of Technology en 1966 (on en trouve un excellent résumé dans Quillian 1967). D’autres contributions importantes ont fait avancer la réflexion sur le sujet (Collins & Loftus 1975 ; Woods 1975 ; Brachman 1979 ; Johnson-Laird, Herman & Chaffin 1984 ; Shastri 1988 ; Mac Randal 1988).
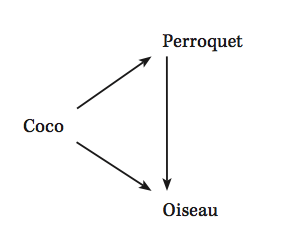
Comment les « réseaux sémantiques » peuvent-ils servir à la représentation des connaissances ? On le comprendra aisément sur une illustration. Imaginons par exemple un réseau composé de trois éléments, « Coco », « perroquet » et « oiseau », et d’une relation, « est un ». Cette dernière est vérifiée entre « Coco » et « perroquet », « Coco » et « oiseau », et « perroquet » et « oiseau ». Soit le graphe présenté dans la figure 1.
La matrice correspondant au graphe est la suivante :
(À proprement parler, la relation « est un » est réflexive : « oiseau est un oiseau », par exemple ; la diagonale principale de la matrice serait alors constituée de « # » et non de « 0 ». Comme le font très justement remarquer Faure et Heurgon : « La réflexivité ne s’obtient souvent que par un artifice de langage. » [Faure & Heurgon 1971 : 7].)
Dans un exemple comme celui-ci, sommets et arcs d’un graphe sont mis à contribution pour représenter les signifiants. « Coco », « perroquet » et « oiseau » apparaissent comme sommets, et « est un » comme arc. La raison pour procéder à cette répartition des tâches, ici entre substantifs d’un côté et verbe et article de l’autre, est que – dans la langue – les substantifs, tel « perroquet » ou « oiseau » apparaissent comme des éléments « stables » entre lesquels les verbes tels « être » semblent établir des relations. Mais, à la lumière des observations faites précédemment, on peut légitimement se demander si ces verbes établissent une relation, ou s’ils se contentent de la signaler, un peu à la manière du yeh chinois dont il était question au chapitre précédent.
Une difficulté qui apparaît immédiatement dans une telle perspective est que le nombre de types de relations va croître aussi vite que le nombre de verbes qui vont être introduits dans le réseau représenté par un graphe :
« Coco demande des graines », exige une nouvelle relation « demander », « Coco chante une chanson », crée la relation « chanter », etc. Les types d’arcs d’un graphe, c’est ce qu’on convient d’appeler ses couleurs, allusion à la convention bien connue de la pratique du tableau noir qui consiste à représenter des choses de nature différente à l’aide de craies de couleurs différentes. Malheureusement, s’il est aisé de manipuler des graphes à une ou deux couleurs, les choses se compliquent considérablement à mesure que le nombre de couleurs augmente. Ceci aurait dû dissuader les praticiens des réseaux sémantiques de répartir au petit bonheur la chance les mots de la langue entre les sommets et les arcs d’un graphe, voire à encombrer encore davantage les réseaux d’indications « métalinguistiques » relatives aux éléments mentionnés (comme les parties du discours [Pollack & Waltz 1986] ou les types de relations existant entre les objets [Sowa 1984]).
C’est pourquoi il est infiniment plus simple de représenter les mots uniquement par des sommets et de réserver les arcs à un autre usage ; ou bien de procéder à l’inverse, c’est-à-dire de représenter les mots par des arcs, et de réserver les sommets. Dans un cas comme dans l’autre, on évite le problème classique des réseaux sémantiques : avoir affaire à des milliers de sommets de nature différente et des milliers d’arcs de nature différente.
Le réseau mnésique
On se souvient que nous avions fait au chapitre précédent une découverte importante sous ce rapport : nous avions constaté que les relations entre signifiants présents dans les enchaînements associatifs spontanés peuvent être regroupées en un petit nombre de familles comme l’inclusion, l’attribution, la synonymie et la connexion simple ; nous avions constaté aussi qu’en français, ces dernières peuvent à leur tour être regroupées en deux types, selon que l’enchaînement s’exprime à l’aide de la copule « être » (« Vénus est l’étoile du matin »), ou du verbe « avoir » dans un usage de copule (« Chéops a une pyramide »).
Qu’on se contente des deux types « est » et « a », ou que l’on recoure aux quatre relations d’inclusion, d’attribution, de synonymie et de connexion simple, le problème de la constitution d’un réseau (de traces) mnésique(s) se trouve considérablement simplifié : deux ou quatre « couleurs » d’arcs si ceux-ci représentent les relations, deux ou quatre types de sommets si la représentation inverse est choisie.
Pour la construction du réseau mnésique du système ANELLA, il a fallu trancher entre associer les signifiants enchaînés aux sommets du graphe ou bien à ses arcs. À notre connaissance, les utilisateurs de réseaux sémantiques classiques ont toujours choisi la première solution : représenter les signifiants enchaînés par des sommets et les relations qui les relient par des arcs. Ce choix s’accorde à la pratique commune intuitive en matière de graphes selon laquelle l’arc représente la relation, et le sommet, l’élément en relation. Nous avons cependant fait pour ANELLA le choix inverse, et ceci pour obtenir deux effets qu’il nous semblait indispensable de reproduire : la délocalisation et la distribution des signifiants.
La délocalisation des signifiants, c’est-à-dire leur situation « entre » tel et tel endroit plutôt qu’« à » tel endroit, semblait nécessaire pour une raison de plausibilité neurophysiologique : on constate en effet, dans les aphasies dues a des lésions graves du cerveau, des dégradations parfois importantes de la performance linguistique, mais jamais la perte de mots individuels, et ceci suggère une inscription « délocalisée » des traces mnésiques. Cette conception a toujours été défendue par les auteurs appartenant au courant associationniste dont Freud fut l’un des représentants atypiques ; c’est lui qui écrivait :
« … les représentations, les pensées, les formations psychiques en général ne sauraient être localisées dans des éléments organiques du système nerveux, mais en quelque sorte entre eux, là où se trouvent des résistances ou des “frayages” qui leur correspondent. Tout ce qui peut devenir objet de perception interne est virtuel, un peu comme l’image produite par le passage des rayons dans une longue-vue. » (Freud 1967 [1900] : 518.)
La délocalisation résulte de la distribution : l’information est fragmentée et encodée en une multitude de localisations. Dans le cas de réseaux de neurones formels, l’information est littéralement « noyée dans la masse » comme dans un hologramme et ne se retrouve en sortie que par « reconstitution coopérative » selon l’expression très juste de Arbib (Arbib 1987 : 95), à la suite d’un processus statistique filtré par les effets de seuil qui interviennent dans chacun des neurones formels.
Pourquoi tenir à ce que le mot soit distribué alors qu’il apparaît typiquement comme une unité stable, pourquoi vouloir que le signifiant « pomme », par exemple, soit distribué au sein d’un réseau mnésique alors qu’il ne l’est pas dans un réseau sémantique ? Imaginons que le signifiant « pomme » soit situé à la fois sur le parcours qui conduit de « poire » à « prune » et sur celui qui conduit de « Adam » à « Ève », eh bien, il est essentiel que ces enchaînements associatifs soient représentés de manière distincte, sans quoi il serait également possible de passer de « poire » à « Ève » ou de « Adam » à « prune », enchaînements associatifs sans aucune plausibilité et dont on sait qu’ils n’apparaissent pas dans la réalité (si ce n’est par ratage). Une autre raison de représenter chaque enchaînement de manière distincte est le caractère crucial – dans la perspective des « dynamique de pertinence » et « dynamique d’affect » qui seront exposées plus loin – que le même signifiant puisse disposer de valeurs différentes pour chacun des enchaînements associatifs où il apparaît. Ce point est développé plus loin (voir chapitre 12), mais on peut l’illustrer tout de suite : il peut être intéressant que le mot « pyramide » dispose de deux valeurs de pertinence différentes selon qu’il se situe dans la suite d’enchaînements associatifs qui conduit de « pharaon » à « tombeau » ou dans celle qui va de « cône » à « tétraèdre » ; de même, il peut être intéressant que le mot « pomme » dispose de deux valeurs d’affect distinctes selon qu’il apparaît entre « poire » et « prune » ou entre « Adam » et « Ève ».
C’est donc bien le même signifiant « pomme » qui est représenté en divers endroits du réseau, mais l’information « pomme » entre « poire » et « prune » est désormais distincte de l’information « pomme » entre « Adam » et « Ève ». La redondance apparente du même signifiant dans le réseau mnésique ne fait que refléter la multiplicité des enchaînements associatifs où il s’inscrit. La génération de phrases en sortie joue sur un seul enchaînement associatif à la fois, et ne nécessite donc aucune « reconstitution coopérative » – comme ce serait le cas pour un système connexionniste statistique : il n’est en effet jamais pertinent que soit reconstituée en sortie toute l’information relative à un signifiant particulier, contenue dans le réseau. L’effet de distribution au sein d’un réseau connexionniste déterministe a donc une fonction très différente de celle qu’il exerce dans un réseau connexionniste classique, c’est-à-dire statistique ou « coopératif » : dans ce dernier, l’information pertinente est effectivement fragmentée entre les « unités cachées » (d’un « perceptron multicouche » [Fukushima, Miyake & Ito 1983] ou d’une « machine de Boltzmann » [Hinton, Sejnowski & Ackley 1984; Ackley, Hinton & Sejnowski 1985]) et doit être reconstituée dans les unités de sortie, alors que dans le premier, la distribution apparente d’une information unique (le signifiant) se révèle être en réalité la distinction des unités d’information effectivement pertinentes (les enchaînements associatifs individuels).


9 réponses à “PRINCIPES DES SYSTÈMES INTELLIGENTS (1989), chapitre 10 (I), réédition en librairie le 23 novembre”
Explications séduisantes et brillantissimes ! Idée des chenaux très intéressante.
Espère avoir assez compris les différents éléments des propositions sémantiques.
Je relirai ce texte par la suite surtout le dernier paragraphe.
Bien à vous, Charles-Henri Batjoens
Stanislas (et non Jean Luc!) Dehaene vs PJ? Je persiste: je vote PJ.
Hi,
Un chenal : Stuxnet – Iran … ouiiii bien ! Stuxnet – Iran – Chevron … Aïe aïe aïe !
« The Worm Turns » As Chevron ‘Infected’ By Stuxnet Collateral Damage
http://www.zerohedge.com/news/2012-11-10/worm-turns-chevron-infected-stuxnet-collateral-damage
Bonsoir Paul
La « synthèse fruitière » de la Genèse: » Une pomme , deux poires , résultat : un tas de pépins » montre que l’on peut bien associer Eve à poire ! Du moins en français populaire!
Ce qui semblerait éliminer les français et sans doute une partie des francophones comme candidats à l’établissement de votre modèle mathématique! Sauf si ce modèle mathématique peut être dérivé du système D!
Ne passez pas le week end dans votre coin de plancher: transgressez les codes comme l’ont fait tous les survivants, laissez vos traces dans la peinture fraîche et appelez ça une « installation » : c’est de l’art moderne, c’est même vendable !
Bon Dimanche
Très cordialement
Un vrai délice, cette série. Aujourd’hui, je me suis rendu compte qu’il fallait ménager son cerveau afin de le conserver en bon état de fonctionnement.
J’avoue que le mien, sûrement à cause de quelques secousses reçues, trouve un chenal bien creusé, direct et sans transbordement, entre bonne poire et Adam ainsi qu’un autre encore plus clair entre Ève et les prunes qu’elle s’efforce à mériter.
« Mais j’ai repeint le plancher de manière à ce point inepte que je vais me retrouver coincé dans un coin de la pièce : l’objet mathématique nécessaire n’existe pas ! Parviendrai-je à l’inventer ? »
Et oui, bon courage.
Très fort ! Vraiment très fort ! Il saute aux yeux que, pour inventer tout ça, il fallait être à la fois un généraliste et un passionné de programmation.
[…] Blog de Paul Jorion » PRINCIPES DES SYSTÈMES INTELLIGENTS (1989), chapitre 10 (I), réédition en …. […]
Je relis…
On retrouve ici le terme de chréode, apparu au chapitre 4 avec référence à Thom (SSM pp. 121 à 123, 1ère ed., 111 à 113 2ème ed.). A la page 124 (resp. 114), Thom écrit:
« Le langage humain est décrit par un modèle sémantique de dimension un (le temps) dont les chréodes sont les mots. »
Je pense que PJ n’utilise pas ici le terme chréode dans le même sens que Thom. Je crois que pour PJ une chréode est seulement ici un enchaînement associatif privilégié, une sorte d’ilôt de déterminisme, alors que pour Thom il y a, en plus, une zone de bifurcation (qu’il appelle zone ombilicale) qui contient une part d’indéterminisme, un éventail de possibles.
Mais je pense qu’au fond, PJ voit les choses comme Thom qui écrit p. 124 (resp. p. 114): « la description complète d’un modèle sémantique exige la donnée de toutes les relations de filiation possibles entre chréodes [ici mots] avec toutes les règles connues qui permettent de diminuer l’indétermination foncière du schéma. »
Je pense qu’on est proche, très proche, des P-graphes (P pour parentalité?) de PJ.