Ce texte est un « article presslib’ » (*)
J’ai présenté en mai deux billets, qui s’appelaient respectivement La dimensionnalité de la monnaie (Introduction) et La dimensionnalité de la monnaie (Reconnaissance de dette et monnaie). Quand l’un d’entre vous m’a demandé récemment où était la conclusion, j’ai répondu qu’elle était malheureusement trop longue pour être présentée ici. Ceci dit, j’aimerais bien connaître vos réactions à mes tentatives exploratoires et c’est pourquoi je reviens sur ma décision et je vous en présente ici, un sommaire.
Il existe en mathématiques, une mesure que l’on appelle la « dimension de Hausdorff ». Sa définition formelle est celle-ci : « La dimension de Hausdorff est un nombre réel positif, éventuellement l’infini, associé à tout espace métrique, c’est-à-dire un ensemble au sein duquel une notion de distance entre les éléments de l’ensemble est définie ».
Ignorons cette définition formelle pour retenir qu’au cœur de la conception qui sous-tend cette mesure, se trouve la notion de distance. Je me contenterai de présenter cette notion de manière très intuitive, sans me préoccuper de rigueur mathématique.
Disons que je détermine sur une feuille de papier, deux points A et B. La distance la plus courte entre ces deux points est, la chose est bien connue, la droite (Figure 1).
Quelle serait la distance la plus longue que l’on puisse imaginer entre ces deux points A et B ? La réponse là aussi est simple : il me suffit de les joindre en faisant un détour par l’infini. Disons que, partant de A je parte vers l’infini vers le haut de la feuille et qu’une fois parvenu là (!), je revienne en direction de B. La distance entre A et B est alors de deux fois l’infini (Figure 2).
Bien entendu, deux fois l’infini, c’est toujours l’infini, mais Georg Cantor en introduisant les nombres « transfinis » à la fin du XIXe siècle, nous a familiarisés avec l’idée d’additionner, voire de multiplier, des infinis.
J’ai donc déterminé d’abord la distance la plus courte entre A et B : la droite, et ensuite la distance la plus longue possible entre ces deux points : deux infinis, l’un à l’aller et l’autre au retour (ou un grand !).
Essayons d’imaginer maintenant un procédé qui nous permettra, partant de la distance la plus courte possible entre A et B – la droite qui les joint – de l’augmenter progressivement.
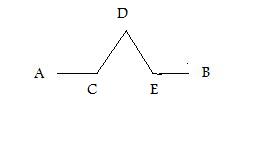
Voici un moyen possible : je divise la droite entre A et B en trois segments et je construis sur la base du tiers central, un triangle équilatéral. Je désigne par C, D, E, les trois nouveaux points d’inflexion sur la ligne brisée qui joint désormais A à B, et je remplace la droite entre C et E par la droite brisée CDE (Figure 3).
Quelle est maintenant la distance entre A et B ? Définissons la distance la plus courte entre eux comme représentant l’unité. La droite brisée CDE, construite comme une « excroissance » sur la droite originale AB est constituée de deux côtés d’un triangle équilatéral. Ceci implique que CD et DE sont tous deux égaux à CE. Or CE est par construction égal à un tiers de la distance AB – c’est le principe qui l’a guidée. La distance parcourue sur la ligne brisée représente donc maintenant quatre tiers de la droite qui joignait originellement A et B. Or nous avions défini celle-ci comme représentant l’unité. Le nouvel AB a donc pour mesure 4/3, soit 1,3333… fois l’unité. La distance entre A et B est donc maintenant de 1,3333…
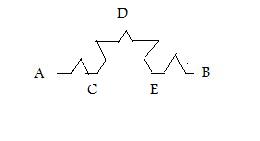
Répétons maintenant l’opération : construisons un triangle équilatéral sur chacun des nouveaux segments AC, CD, DE et EB (Figure 4).
Qu’est devenue la distance entre A et B ? AC représente maintenant quatre tiers de l’ancien AC qui était lui-même un tiers de 1, de même pour le nouveau CE, le nouveau DE et le nouveau EB. On a donc maintenant entre A et B, quatre fois 1,3333… fois un tiers de 1, autrement dit : 4 x (1,3333… x 0.3333), c’est-à-dire : 1,7777… (ou 16 / 9).
Nous avons donc, à l’aide de nos constructions successives, augmenté la distance entre A et B. En répétant la même opération, nous multiplierons à chaque fois la distance déjà obtenue par 1,3333… La distance entre A et B à partir d’une ligne brisée construite de cette manière continuera donc d’augmenter inexorablement (par un facteur de 4 en numérateur et par un facteur de 3 en dénominateur) si l’unité reste définie comme la distance que représente la droite que l’on peut tracer entre A et B.
Le concept de « dimension de Hausdorff » est apparenté à la mesure que je viens de définir. Différence essentielle, la dimension de Hausdorff d’une ligne, aussi compliquée soit-elle, ne dépassera jamais 2 qui est la mesure correspondant au « remplissage » total d’une surface, alors que le concept de distance que je viens d’introduire permettrait lui d’atteindre une dimension infinie puisque chaque nouvelle « complexification » conduit à une multiplication par un facteur de 1,3333… La raison exacte pour laquelle ces deux dimensions diffèrent n’a pas d’importance, ce que j’entendais faire, c’était offrir une compréhension intuitive de la notion de « dimensionnalité ».
Dans le cas de l’apologue de la Dame de Condé, nous comprenons intuitivement qu’il existe une différence significative entre une situation où aucun des habitants du village n’a contracté de dette envers aucun autre, et une autre où un réseau complexe de reconnaissances de dette les relie entre eux. La « complexité » de la structure de crédit entre les habitants du village exprime aussi la fragilité de la communauté sur le plan financier car le défaut de l’un dans le remboursement de sa dette risque de précipiter le défaut d’un autre, déclenchant ainsi une réaction en chaîne.
Définissons maintenant les éléments dont nous aurons besoin pour mesurer la « dimensionnalité » du crédit au sein d’une communauté. La somme de monnaie fiduciaire – l’argent disponible – sera l’étalon, la valeur dont on part : l’équivalent sur le plan monétaire de la « distance la plus courte » dans l’illustration que j’avais proposée. La somme des reconnaissances de dettes au sein de la communauté mesurera elle la « distance de la dette ».
La complexité minimale sera celle d’une situation où nul ne doit d’argent à quiconque, et la complexité maximale correspondra à celle où chacun doit tout l’argent qu’il a à d’autres villageois.
Nous allons additionner la monnaie fiduciaire disponible aux reconnaissances de dette mais pas dans une optique où il s’agirait de deux manifestations de la même chose, autrement dit que les deux constitueraient « de la monnaie » sous une forme ou une autre, non : nous les additionnons dans une perspective où il s’agit de choses bien différentes et où l’une, l’argent, la monnaie fiduciaire, est un moyen neutre de faciliter les échanges (dans ce contexte en tout cas !), alors que la dette, constituant elle un facteur de risque, est essentiellement dangereuse. Pour obtenir une jauge du degré de péril et donc de la fragilité d’un environnement financier, nous allons donc créer un indice sur le même principe que la dimension de Hausdorff : nous allons comparer la valeur de la dette à celle de l’argent disponible. Pour obtenir une mesure qui, comme dans le cas de la dimension de Hausdorff, peut prendre des valeurs qui varient entre 1 et 2, il nous suffit de diviser la somme de la dette d et de l’argent disponible a par l’argent disponible. Dimension créancière : (d + a) / a.
Soit x la somme de l’argent disponible. Si personne n’a de dette envers personne, la dimension créancière est de
(0 + x) / x = x / x = 1
Si au contraire tout le monde doit tout l’argent qu’il a (à une ou à plusieurs personnes), la dette vaudra x, tout comme l’argent disponible, et la dimension créancière sera de
(x + x) / x = 2x / x = 2
Dans le cas de l’apologue de la Dame de Condé qui nous a servi de point de départ, la somme des dettes dues par l’ensemble des commerçants connectés entre eux par un réseau de reconnaissances de dette, préalablement à la visite de la Dame, est de 600 €. La dette sera tombée à zéro après son départ. La valeur de la dimension créancière à Condé après le départ de la Dame est de 1 puisqu’on a :
(0 + x) / x = x / x = 1
et ceci quelle que soit la valeur de x, l’argent disponible dans le village. Mais la valeur de la dimension créancière à Condé avant la venue de la Dame ne peut pas elle être déterminée a priori puisqu’elle dépend aussi de la valeur de x : elle dépend de ce que ces 600 € représentent par rapport à l’argent disponible à Condé. Il pourra s’agir en effet, selon les cas, d’une somme considérable par rapport à l’argent détenu par les habitants du village ou ne représentera au contraire qu’une somme minime pour eux. Prenons deux exemples : dans le premier, la fortune totale de la communauté est de 1.200 €. Dans ce cas, la dimension créancière est de
(600 € + 1.200 €) / 1.200 € = 1.800 € / 1.200 € = 1.5
Dans le second exemple, la fortune totale est de 5.400 €. Dans ce cas, la dimension créancière est de
(600 € + 5.400 €) / 5.400 € = 6.000 € / 5.400 € = 1.111…
Quel est la portée de la mesure qu’introduit une dimension créancière, comparable à la dimension de Hausdorff ? Raffinée, elle offrirait un outil de rechange à ce que tentent maladroitement de mesurer les différentes définitions de la masse monétaire M1, M2, M3 qui reflètent de manière très indirecte le double emploi, le triple emploi, etc. qu’opèrent les reconnaissances de dette par rapport à l’argent.
On l’a vu, il y a, implicite aux définitions de ces masses monétaires M1, M2, M3, une représentation supposant que les reconnaissances de dette constituent « de la monnaie », et ceci du fait qu’une fois endossées, elles sont effectivement des marchandises et ont une valeur à ce titre, ce qui les rend partiellement substituables à de l’argent. Cette assimilation des reconnaissances de dette à de l’argent, je l’ai, comme on l’a vu, rejetée, parce qu’elle suppose pour être valide, un contexte économique idéal. Dans un cas de crise du système économique, comme celle que nous traversons en ce moment, la valeur de ces reconnaissances de dette s’écarte de manière dramatique de leur valeur nominale, pouvant même tomber à zéro.
Il serait faux cependant d’ignorer les reconnaissances de dette dans une évaluation globale de la situation financière : il faut les évaluer, comme je l’ai montré précédemment, de manière conditionnelle : en les affectant d’un coefficient mesurant la disposition effective de ces sommes à être recouvrées. Mais il faut aussi, et en réalité surtout, mesurer leur impact du fait de leur capacité – au contraire de l’argent, c’est-à-dire des pièces au fond de nos poches et des billets dans nos portefeuilles – d’engendrer de l’intérêt, c’est-à-dire d’exiger en paiement des sommes qui devront être trouvées ailleurs. Et c’est ici qu’intervient, de manière cruciale, la distinction sur laquelle je me suis appesanti entre prêts à la production qui, servant d’avances et générant de nouvelles richesses, prennent soin des intérêts qui devront être versés à celui qui a avancé le capital, et prêts à la consommation, qui doivent eux puiser les sommes nécessaires au versement des intérêts dans une richesse créée dans un contexte tout différent : comme salaires essentiellement.
(*) Un « article presslib’ » est libre de reproduction en tout ou en partie à condition que le présent alinéa soit reproduit à sa suite. Paul Jorion est un « journaliste presslib’ » qui vit exclusivement de ses droits d’auteurs et de vos contributions. Il pourra continuer d’écrire comme il le fait aujourd’hui tant que vous l’y aiderez. Votre soutien peut s’exprimer ici.

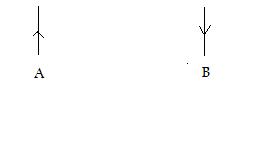
50 réponses à “La dimensionnalité de la monnaie (La dimension créancière)”
@Paul Jorion
Tout comme logique, j’ai été tout d’abord intrigué par la dimension fractale. Puis déçu parce que la dimension créancière n’est en rien fractale, ni même une dimension, mais un simple ratio, càd un pourcentage sans dimension. Par ex. c’est du même ordre que le niveau de la dette publique / PIB.
Cela n’enlève rien à la pertinence de cette variable sans dimension. Mais, il y a un peu de confusion mathématique, il me semble.
Monsieur Jorion,
Merci de m’avoir répondu.
J’ai lu le message à cette adresse http://www.pauljorion.com/blog_en/?p=44. D’accord pour l’introduction d’une variable « profit » dans les volatilités. La forme du sourire correspond bien à un profit minimal demandé par l’opérateur. Je ne sais rien du modèle de Black-Sholes, donc je n’en dit rien. Mais je vous fais confiance. Vos critiques « définition circulaire de la volatilité et manquer une variable (ce point est clair pour moi) » anéantissent ce modèle. Des erreurs de cette gravité sont étonnantes.
Pour l’histoire de la courbe normale, Mandelbrot s’est beaucoup amusé à la détruire dans (je crois) « les Marchés Fractals ». Ce livre doit dater de 1995. Taleb n’est pas seul. Que les ingénieurs financiers soient au courant de ce problème ne m’étonne pas.
Maintenant, je prends ce problème et celui des bulles pour dire que la confiance accordée aux mathématiques était exagérée. Un non mathématicien qui voit un modèle mathématique sans le comprendre est très souvent impressionné et se dit que cela représente forcément la réalité. Je la résume par « C’est mathématique, donc il n’y a pas d’erreur. On peut lui faire aveuglément confiance ». C’est, à mon avis, une erreur.
Mettez les prédictions des modèles et l’avidité ensemble et évitez, par incompréhension ou par manque de temps, de vous assurer de la validité des hypothèses de base (hypothèses fausses ou appliquer le modèle à des objets totalement imprévus par le concepteur, ce qui revient au même). Accélérez les opérations pour des questions de compétitivité. Cela donnera des problèmes.
J’imagine que par les modèles mathématiques, les financiers avaient des réponses à des questions du genre : « Je gagne quoi si j’achète ce truc? » ou « Quel est le prix de ce machin dans une semaine? » La réponse était un nombre. Si ce nombre était assez haut et avec une assez grande probabilité pour son goût, le trader se mettait à parier sur la somme d’argent qu’il allait se faire. Il pouvait utiliser les résultats d’un engagement en cours pour s’engager ailleurs. Il pouvait allonger le « chenal » d’utilisation de l’argent disponible. Cela me laisse rêveur.
Il y a mieux. Dans les produits financiers modernes, le même débiteur partage le risque qu’il représente sur plusieurs « véhicules (?) » et le créancier ne supporte qu’une toute petite partie du risque que ce dernier représente. En théorie, c’est superbe. Chaque débiteur est indépendant des autres. Mathématiquement, la probabilité que la majorité des débiteurs coule, est ridiculement faible et plus il y en a plus cette probabilité diminue. En théorie, je ne vois aucune raison de se limiter. Les notes AA deviennent de plus en plus solides avec l’extension du système. Un monde « parfait » est en vue.
Les « chenaux » ont été allongés dans une sécurité trompeuse. Ils ont été mélangés. L’hypothèse d’indépendance saute. Au moindre doute, le prix de ces produits financiers devient douteux. Cela perturbe toute la chaîne des engagements et contamine les engagements liés à celui qui est devenu douteux. Comme ils sont liés, ce n’est plus un problème isolé. Les fameux appels à la confiance deviennent sensés. Si elle est rétablie, cela repart. J’y vois là l’idée des plans de relance US. Le système est théoriquement parfait.
M’enfin faire des paris sur des propabilités c’est toujours risqué. Car il y a une propabilité qui dans le temps s’inverse ou croit plus lentement, c’est celle des prix. Le prix ne peuvent pas monter jusqu’aux ciel et cette propabilité est de 100%. Donc faire un modélé en integrant l’augmentation constante du prix des actifs n’est qu’une pure fiction. Le système théorique est inparfait puisqu’il ne prend pas en compte les maximums. Ont le voie bien avec les quantité de dette et les ratios. C’est pour cette seule raison que les économiste ont peur de la déflation, car dans se cas précis la valeur des actif et des réserves en actif font tout plonger. Les gens se déleste de leur position et la mécanique s’inverse. Mais encore une fois la notion d’abus n’est pas un paramétre utilisé dans les modèle et du coup les modèle sont pipé des le départ.
@Paul Jorion
je n’ai pas fini de lire l’article, mais pour le début vous devriez carrément vous inspirer de la notion de dimension fractale : http://fr.wikipedia.org/wiki/Dimension#Dimension_fractale
@Paul Jorion
Heu oui comme Fujisan, après avoir lu la fin, je ne vois pas le rapport entre l’introduction aux « dimensions » alors qu’il ne s’agit que d’un ratio dans la suite du raisonnement.
Ca donne une impression d’inutilement alambiqué.
D’autre part l’aspect temporel de la reconnaissance de dette est totalement ignoré, de même que l’aspect fiduciaire, alors qu’ils me semblent être le coeur du problème / mystère de la monnaie.
C’est bien l’immédiateté de la monnaie qui la différencie de la reconnaissance de dette, ainsi que la confiance totale qu’on lui accorde. Non ?
Ces aspects pourrait donner lieu a des dimensions fractales lorsqu’on combine via la titrisation et autres artifices financiers. C’est peut-être prématuré par rapport à votre cheminement, mais puisqu’on en reste encore à de « ‘intuitif » et pas a du mathématiquement rigoureux, j’ose m’y aventurer un peu.
1 – l’introduction sur la dimension de Hausdorff est distrayante et claire mais trés longue et peu utile
2 – l’utilité de ce nouveau concept de dimension créanciére est a peine esquissée alors que c’est un préalable indispensable.
3 – Pourquoi ne pas se contenter d’un truc moins bluffant comme le ratio dette/(argent disponible) ou la disponibilité créanciére = 100 X (dette + argent disponible)/(argent disponible). La disponiblité créanciére est evidemment identique à la dimension créanciére mais en plus humble.
c’est rigolo, les réflexions de « logique »…
l’auteur du blog et lui, on dirait le Don Quichotte et Sancho Panza :
la bataille avec les fumeux moulins à vent de la Théorie versus le bon sens terre-à-terre
en troisième position, Hercule Poirot, le futé…
Génial ! Cet article nous montre une nouvelle planète finance, il ne faut pas le lire au pied de la lettre. Pour tenir dans le format blog, et ne pas rebuter ses lecteurs, Paul présente l’esquisse d’une idée radicalement nouvelle et, de mon point de vue, nécessaire : introduire en économie une notion d’espace qui soit adaptée à ce qu’elle est devenue. Autrefois, l’espace géographique suffisait car les échanges et les risques étaient surtout d’origine physique, mais aujourd’hui ça ne colle plus : devenus interdépendants de façon abstraite par le truchement de titres innombrables, les acteurs financiers n’existent plus que dans un espace abstrait. A l’origine, le mot marché renvoyait à un lieu bien précis que l’on retrouve en toponymie, (c’est la très courante « place du marché »), aujourd’hui il n’existe plus nulle part : donc il n’existe pas strico sensu, Cf. Aristote : « Ainsi tout le monde admet que ce qui est, est en quelque lieu de l’espace, et que ce qui n’est pas n’est nulle part; car où sont, par exemple, le bouc-cerf et le sphinx? » (Livre IV, chapitre I, §2)
Il y a tout, dans cet article, sauf une clef pour en saisir la portée : une base de temps. Il faut oublier les bases usuelles qui nous font calculer des montants totaux, et se rappeler que, en pratique et en règle générale, une reconnaissance de dette donne lieu à des versements à échéances cadencées. Ainsi, les petite formules de Paul s’expliquent très bien : si, à telle échéance, un acteur doit payer plus que « tout l’argent qu’il a », alors soit il est insolvable, soit il doit vendre une partie de ses biens. Bien plus qu’un banal ratio, c’est un indicateur très rationnel pour signaler un début de crise, car vendre un bien pour payer une traite n’a rien de « normal », donc rien de rassurant : c’est la preuve que les revenus ont diminué, ou que d’autres dépenses ont augmenté. Les prêteurs de subprimes, qui misaient sur la vente des maisons pour se rattraper, faisaient un mauvais calcul.
Le temps joue un grand rôle que l’on sous-estime. Le village visité par la Dame de Condé s’en tire à bon compte puisqu’un seul billet permet à tous les endettés de rembourser leur dette. Mais introduisons des échéances : il suffirait, selon les cas, qu’elle passe un jour trop tard pour que les mêmes se retrouvent tous en défaut de paiement, donc contraints à vider leur grenier et vendre son contenu sur la place du marché. C’est une invitation à concevoir un espace-temps fractal puisque fractionné par nature : entre deux échéances, il importe peu que l’on soit riche comme Crésus ou pauvre comme Job, seul importe le fait de pouvoir payer les traites à échéance, comme des musiciens placent leurs notes dans le bon tempo.
Quoiqu’il en soit, je remercie infiniment monsieur Jorion pour cet article qui me fait rêver.
J’aime cette approche fractale qui donne une meilleure idée de la distance qui se multiplie sur un rythme exponentiel. Ok pour la dimensionnalité dans le sens de distance, mais il me manque comme une notion de complexité des dettes, noeuds dans les fils reliant les personnes.
Dans l’approche fractale comme dans le livret blanc de bernard lieater, on retrouve cette idée de performance où l’on va essayer de pousser au maximum la machine (changeant la dimensionnalité et augmentant le risque) jusqu’au krach. L’aspect de différence de qualité entre les deux me fait penser au niveau du flotteur entre la partie émergée de l’iceberg et immergée.
Pour éviter un krach de l’économie, il nous faut une économie de secours pour pouvoir jongler de l’une à l’autre, selon leurs états, puisque ce sont des crises monétaires, et de crédits que nous avons, créons une économie, un système parallèle composé de monnaies complémentaires avec des règles différentes, sans intérêts, avec moins d’intérêts, avec une limite dans la dimensionnalité, avec des monnaies fondantes (pour jf), avec un système rothbardien, ayons dans nos livres de comptes et nos porte monnaies ou en digital, tout un panel de monnaie de secours, dans un premier temps qui puissent reprendre le flambeau quand la grande économie capitaliste dérape en voulant trop pousser la bête.
C’est le cas du WIR qui sert de 2ème roue au système bancaire suisse.
J’ai posté à ce sujet aujourd’hui sur mon blog une vidéo de Margrit Kennedy sur le non sens des intérêts et les solutions que représentent les monnaies complémentaires locales : http://www.zoupic.com
Je laisse de côté les mathématiques qui ne sont de toute façon utilisées ici que de manière intuitive ou mieux analogique.
Ce n’est pas tant que certaines choses sont en trop. Mais plutôt qu’il en manque certaines je pense.
– S’agit-il simplement de la construction d’un nouvel indicateur?
– S’agit-il d’expliquer « un monde » (le village)? Celui-ci n’est possible qu’à condition que X, Y, Z aient telle ou telle propriétés ou qu’il y ait telle ou telle hiérarchie dans les critères déterminants X Y et Z, différentes de ce que la théorie retient habituellement?
– S’agit-il, de manière encore plus fondamentale, de présenter une nouvelle façon d’intégrer la notion du temps à celle de monnaie et de reconnaissance de dette?
Comme crapaud rouge je crois qu’il y a là plus que la recherche d’un nouvel indicateur. Il y a dans cet article une thèse sur la façon la plus pertinente de concevoir le TEMPS lui-même lorsqu’on aborde ces questions, façon de concevoir le temps qui est en totale opposition avec la façon dont les économistes/financiers le traitent habituellement.
Faut que j’y réfléchisse mais malgré les apparences on s’éloigne d’une représentation spatialisée du temps.
Contrairement aux apparences donc, il ne s’agit pas ici d’une mathématisation de plus.
Je dirais pour conclure:
1/ L’approche ouvre des perspectives intéressantes, en théologie politique comme en philosophie politique.
2/ Il faudrait recenser (j’ai honte de ne pas l’avoir fait au fur et à mesure) les différentes façons dont le lien entre temps/monnaie/ crédit/ communauté ont pu être envisagées sur ce blog, et voir si elles sont toutes mutuellement compatibles ou pas.
Merci à tous.
Logique,
Merci pour votre intervention. Le monsieur, dont vous avez perdu le nom, est Benoit Mandelbrot. C’est un mathématicien qui a, selon ses dires, découvert les fractales par ses tentatives de modéliser l’évolution des marchés financiers.
Il s’est beaucoup amusé à attaquer l’ingénierie financière classique.
En ce qui concerne la complexité, ma conviction est qu’un modèle tout simple peut contenir une quantité hallucinante d’informations. Si vous considérez la droite des réels, il s’y trouve un objet géométrique, tous les nombres réels, des vecteurs que vous pouvez associer à chaque nombre réel, des fonctions associables à chaque transformation (aussi un vecteur) applicable à n’importe quel nombre et même des objets géométriques lorsque vous considérez des opérateurs comme x^2+y^2=R^2. R^2 est ici un nombre réel, qui à travers l’opérateur représente un cercle centré à l’origine d’un repère cartésien du plan. Bref, c’est long…
Ensuite, votre idée d’intégrer les « dimensions » politique, économiques, sociales et environnementales dans un modèle mathématique est très ambitieuse. L’une de ses difficultés est l’obligation de tout mesurer. Si c’est possible, cela représente une quantité hallucinante de nombres à agréger dans ce modèle. Essayez simplement de quantifier tout ce que vous faites dans la journée.
Un bon modèle, à mon avis, est aussi simple que possible, aussi versatile que possible et tout de même proche de la réalité. Si ses prédictions se vérifient, c’est un bon modèle. Il devient passionnant si des choses invisibles (pas d’outils pour les observer) deviennent visibles. Il devient utile s’il permet de prendre des décisions pertinentes dans le fouillis de la réalité.
Je m’emporte. La question de la modélisation m’intéresse.
Louise,
Merci pour votre intervention. Votre remarque sur les dimensions finies de la terre relève du bon sens. Cette précieuse denrée a de la peine à entrer dans un modèle mathématique. Dans cette science, 10, 100, 1000, 10000 et 100000000000 sont équivalents. Si ce sont des Euros, je reçois avec plaisir le dernier nombre. J’ai le premier en poche.
Vous avez raison avec l’idée de la concentration des richesses. C’en est au point qu’un ministre allemand a menacé les banques de leur forcer la main si elles gardent tout pour elles.
Soignez votre grippe. Je vous souhaite un prompt rétablissement.
A Didier
Merci beaucoup, pas encore tout à fait remise mais ça s’améliore.
Je constate que ça s’agite sur ce blog, ça grouille de partout.
J’y réagis depuis peu de temps, je n’y connais rien en bourse, ni en finance, (j’ai l’équivalent d’un cap d’aide comptable), mais je possède un cerveau « matheux » qui me permet sans vraiment les comprendre d’appréhender certains concepts, ajoutez à cela un solide bon sens issu d’origines « terriennes » et vous comprendrez que pour moi certaines élucubrations ont du mal à passer.
A propos des jeunes pousses par exemple j’ai posté je ne sais plus où ni quand, quelque chose qui disait en gros que sur un sol en voie de désertification il était difficile de faire pousser quoi que se soit sans un engrais approprié ce qui me semble être du bon gros bon sens élémentaire de base, n’importe quel agriculteur vous le dira.
@Louise
le cerveau « matheux » est plutôt déductif par nature, vous c’est plutôt le raisonnement inductif que vous utilisez … mais ca n’a pas grande importance 😉
@Didier,
Non ce n’était pas mendelbrot pour se coup, mais il avait lui aussi une approche fractal. Par contre il y a des outils assez simple pour modéliser des models avec beaucoup de paramètres, ce sont les matrices. Sinon comme je l’ais dit il y a un modle neuronal, que j’ais devellopé qui pourrait trés bien modeliser des structure 3D dans le temps.
Si cela vous interresse, Paul peut vous donnez me vrai adresse email, je me ferais un plaisir de tenté de vous l’expliquer.
M’enfin avec X Y Z ont peut deja facilement définir en X l’épargne en Y le crédit est en Z le temps. Mais il faut les outil necessaire a cette forme de représentation. Sur le papier ont peut le faire en perspective. C’est deja un bon debut. Le problème sourvient lorsqu’il faut tracer la suite temporel des operations. A ce momment la X Y Z doivent faire partie d’un neurone informationnel qui peut être modeliser par une matrice. Oui chaque vecteur XYZ d’une matrice se voit connecter a un ou plusieurs autres vecteur d’une autre matrice. Dans se cas la matrice représente la Banque ou un particulier qui veut suivre son épargne qui aura été prété.
C’est pas si compliqué a faire mais il faudrait deja trouver un moyen d’organiser les informations. Mais là fait se qu’il faut a vrai dire.
J’espère ne pas avoir été trop confut.
A ybabel
Je dois faire des déductions inductives ou des inductions déductives c’est selon (ouarf, ouarf!!!)
à Logique
N’est t-on pas en train de clarifier la façon de découper en tranches
l’agglutination démentielle et diabolique des topBanques-à-tout-faire y compris toutes les formes d’assurances et toutes les formes de Bourse, émissions d’actions et obligations, gestions de patrimoines, etc. etc.
Une fois que la nomenclature de découpage sera établie,
il faudra que les « N » formes hétérogènes spécialisées
soient aisément geolocalisables dans les villes « places financières :
Bâle, Londres, Bruxelles, Riyadh, Dubai, Hong-Kong, Singapour, Francfort, New-York, Chicago, Zurich, Genève, Luxembourg, Edinbourg, Tokyo, Moscou, Paris et quelques autres.
Demandez à Barbe-toute-bleue et Coucou — Le temps qu’il fait, le 22 mai 2009 —
réunissant Tableaux Sources & Emplois de Fonds.
Pour évaluer les inter-relations, éliminations 2-à-2, consolidations, etc.
le travail ne peut se faire que dans l’arborescence classique d’un PC et à plat sur une table.
Donc sans 3D ni dimensions extra-terrestres pour astronomes.
Voyez-vous la manoeuvre pour LeClownBlanc ?
@antoine,
merci pour le lien je n’avais pas eu l’occasion de voir les tableaux. petite période de banissement et de confision. C’est clair qu’avec un bon tableur ont peut faire beaucoup de chose.
une fois que lon sait se que l’on désire représenter, on a la choix de l’outils de representation. c’est vrai qu’avec un bon tableur ont peut deja faire beaucoup de chose.
@paul jorion et crapreau rouge
Une question m’empeche de dormir :
Si l’on integre les intérets et les echeances (ou le temps), ne se confronte t on pas a une realité quasi quantique : a chaque échéance (ou a chaque instant), le seul fait de determiner la dimension creanciere influe sur celle ci puisqu’en résolvant l’équation on révèle ou un etat d’insolvabilité qui fait lui même varier la valeur attribuée aux reconnaissances de dettes (qui n’ont plus aucune valeur si il ya insolvabilité du système) et donc la dimension creanciere?
D’autre part que se passe t il lorsque l’insolvabilté est prononcée? D’ou peut on sortir le billet de la dame machin pour boucler la longue chaine (fractale) qui relie tous les entre-endettés? certainement pas du stock de billet qui représente l’argent disponible (on se retrouverait encore plus endettés!). Des matières premières semble la seule réponse. Donc le surendettement du système est en train d’hypotéquer les réserves de matière première dans lesquelles on peu inclure la main d’oeuvre (et/ou les impots). Les banques et les etat ne sont ils pas en train d’organiser l’esclavage des masses en les contraignant a plus de travail de croissance pour moins de pouvoir d’achat? Aujourd’hui travailler plus pour gagner plus, demain travailler plus pour rembourser la dette… ou pour beneficier d’un peu d’eau, de gasoil et de 3 grains de blé?
bonne nuit quand même.
Monsieur,
je trouve que vos manières sont convenables.
En plus les détours mathématiques sont pleins de sens, alors qu’en économie les Nobel ne voyaient science…
Pourriez-vous, s’il vous plaît, m’indiquer une adresse où je puisse faire contribution à la tenue de votre blog en argent liquide?
Je sais que cela est très peu orthodoxe, mais étant interdit bancaire, je n’ai d’autres moyens subtils, étant donnée la distance!
Bien entendu, je confirmerai par mail la consistance en argent de ces contributions.
Ainsi, toute comptabilité tenue pourra l’être.
Merci votre blog.
Ce qui fait la richesse,étant la valeur de ce que l’on possède,chacun se trouve dans la crainte de perdre de la valeur,et de s’appauvrir(qu’elle horreur!).I ne reste plus qu’a déplacer les billes(que l’on à piqué aux autres……..nous) le plus rapidement possible pour les placer là ou la valeur est la plus haute.D’où le retour à des valeurs refuges comme l’or(les lingots par exemple),certaines matières premières,les nouvelles technologies,l’immobilier.Chacun se refourguant les reconnaissances de dettes comme une grenade avant qu’elle n’explose.Pour gagner du temps on fait marcher la planche à billets.
Les monnaies à ce jeu là vaudront moins qu’un billet de monopoly.Ou bien?
En physique un tel écart de rapport de force et de temps entre deux états dépendant l’un de l’autre: le monde de la finance et l’économie réelle ne peuvent qu’aboutir à une rupture.
A jouer avec l’outil mathématique dans le tube à essais de sa propre pensée ,on se prend pour le gars qui à découvert le fil à couper le beurre(moins dangereux………..à l’échelle globale…plus simple et plus utile).
Il est des outils que l’on ne met pas dans les mains d’un enfant.L’intelligence mathématique mal employée par des primates surdoués se prenant pour des dieux et voilà le travail.
Le génie conduit parfois,à une forme de pathologie mentale,une hypertrophie d’une capacité au détriment de toutes les autres.
On ne peut qu’être en colère quand on songe au prix en vies humaines broyées a ce jeux et au gaspillage de tant d’énergies,par un détournement,une perversion des sciences.Quel gâchis!
« Science sans conscience n’est que ruine de l’âme »……c’est peu dire!
A vous lire tous ,on ne peut que garder espoir,il y a des personnes qui ont une tête,une conscience et qui oeuvrent partout ou ils sont.
Par la convergences des intelligences et des « hommes de bonnes volontés, »nous arriverons bien à réinventer un modèle économique et social digne de notre humanité.Chacun à son niveau avec ses compétences.
Désolée pour le ton de mon intervention ,pas très constructive.Ce soir je n’ai pas le moral.
Ce blog est comme une trouée de lumière dans le ciel qui s’assombrit.
Une question me taraude: Comment se fait-il que les analyses de Monsieur Paul Jorion sur BFM radio ne soient pas relayées dans les autres émissions comme celle des « experts »?
Puissions nous contribuer à limiter la casse……… et passer entre les gouttes.
Au plaisir de vous lire.